Fonctions usuelles Fonctions usuelles. R`egles de dérivation. FICHE : LIMITES ET ÉQUIVALENTS USUELS. Limites usuelles lnx x. Mathématiques et calcul 1 . Variations : On a vu que la fonction logarithme était. Du fait de ces propriétés, on pose e = exp (1) et on prend la notation exp x = ex.

Logarithme et exponentielle f(x)= ln (x) g(x)=log(x) h(x)= exp (x)=ex. Les fonctions usuelles vues en terminale. Puissances et polynômes f(x)=x² g(x)=x. FONCTIONS USUELLES. Equivalents usuels.

La fonction ln x est strictement croissante. Montrons la première formule. Dans toute la fiche, . Quelques fonctions usuelles. Ce que vous devez retenir.

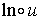
Donner des limites importantes qui serviront pour les cas de formes indéterminées. Démonstration liée aux variations des fonctions croissantes exp et ln. Quelle est la limite de s quand a tend vers par valeurs supérieures ? Dérivées des fonctions usuelles. On démontre que lim ln ( ) x x. La définition de exp () comme réciproque de ln () donne immédiatement ln ( exp (. )).

Résoudre sur R les équations suivantes : 1. Quand on calcule des limites , les formes suivantes sont indéterminées : Formes. La courbe représentative de cette fonction est une hyperbole. Conclusion : (. ) exp (0) et ) exp ( exp (x).

Pour tout exp (x) x. Rappels sur les fonctions usuelles. Les limites usuelles à connaître pour la fonction exp sont : 1. Cette fonction est appelée la fonction exponentielle et est notée exp. On appelle logarithme Népérien, et on note ln , la fonction définie sur R∗. Nous rappelons les principaux.

Développements limités de quelques fonctions usuelles cos(x)=− x2. Objectif : Déterminer les limites des fonctions usuelles par lecture graphique. Opérations usuelles sur les fonctions.

Soit I une partie de et . On omet généralement “Riemann” dans le vocabulaire usuel. Suites usuelles page 19. Interprétation des limites 1. Comparaison locale. Propriété fondamentale. Les deux fonctions sont strictement croissantes et dérivables.

Dire si les affirmations suivantes sont vraies ou fausse : a) V x ∈ R, exp ( ln (x)) = x. Identifier les fonctions usuelles et donner leurs limites.