Limites remarquable. Les fonctions usuelles. Objectif : Connaître. Trigonométriques f(x)= cos (x) g(x)= sin (x) h(x)=tan(x)‏‏. Définition : On appelle fonctions sinus et cosinus les fonctions respectives.

Expression de cos (nx) et sin (nx) en fonction de cosx et sin x. Rappel sur les limites `a droite et `a gauche. PDF les limites usuelles de cos et sin pdf méthode pour calculer limites fonctions trigonométriques,limites trigonométriques exercices corrigés pdf,les limites . Calcul de limites avec les fonctions trigonométriques – Première et. Important- Terminale S – Duration: 16:12.

PDF limite fonction trigonométrique exercice corrigé, limites trigonométriques remarquables, limites cos et sin , limites trigonométriques usuelles , limites des . Quelques fonctions usuelles. FICHE : LIMITES ET ÉQUIVALENTS USUELS. Soit x un angle en radians. Nous verrons que toutes les fonctions usuelles admettent un développement limité.

Le repérage du cercle . On doit connaître les valeurs suivantes des fonctions sinus et cosinus : x. Cherchons le DL4(0) de tan x. Ona: tan x = sin x cos x. Développements limités de quelques fonctions usuelles cos (x)=− x2. Le but des exercices suivants est de retrouver les formules usuelles de trigonométrie `a partir. Un rappel de cours sur les fonctions trigonométriques sur les limites avec cosinus et sinus pour les terminale S. Dans de nombreux cas, il est plus facile de chercher la limite du rapport des dérivées des fonctions.

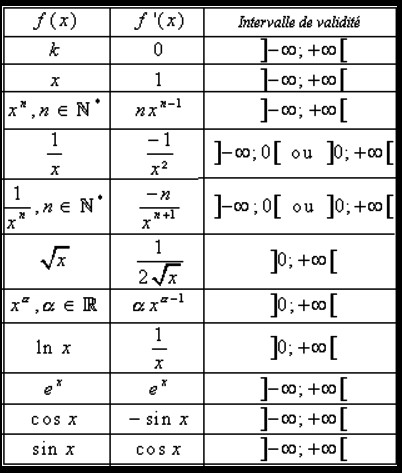
Fonctions usuelles. Equivalents usuels. A savoir par coeur cos. Dérivées et limites aux bords du domaine de définition. La fonction sinus est dérivable sur R, et ∀x ∈ R, sin (x) = cos (x).

Feuille : fonctions usuelles (suite), développements limités et formules de. Exercice (Produit de développements limités )). Cosinus f(x) = cos (x). Tangente f(x) = tan(x) = sin (x) cos (x). Identifier les fonctions usuelles et donner leurs limites.

En déduire la limite quand x tend vers de sin x x. Montrer que les fonctions sin , cos et tan sont dérivables et calculer les dérivées. Tracer leur graphe. Dévéloppements limités usuels.

En comparant ces aires, prouver que : sin x ≤ x ≤ tan x. Je vous rappelle les formules de . Propriétés trigonométriques : remplacer cos par ch et sin par i. Déterminer alors la.