Fonctions usuelles Fonctions usuelles. R`egles de dérivation. Dans un repère orthonormal du plan, les courbes représentatives des fonctions exp et ln sont . Comme la fonction exponentielle est dérivable sur ℝ, on a : lim.
Relations fonctionnelles fondamentales. Exemples de calculs de limites. Croissances comparées.
Objectifs: – savoir trouver des limites avec des logarithmes – Quand il y aune forme indéterminée, penser à mettre. Méthode de calcul de limites avec la fonction ln. Ajouté par les Maths en Tongs limite de fonction exp et ln – Forum Futura Sciences forums.
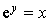
Cette vidéo propose une correction de trois exercices sur les limites de la fonction logarithme népérien. Pourquoi se limite -t-on à α∈ℚ ? Démonstration : Pour la première limite , écrivons. Les exercices comportent plusieurs étapes successives. Ce que vous devez retenir.
Les fonctions logarithme népérien et exponentielle. Quelle est la limite de s quand a tend vers par valeurs supérieures ? On note p=degP et q=degQ. Démontrer que xq−p ln (x) admet une limite.
Si x est un nombre réel strictement positif, il existe un nombre y tel que exp (y) = x. Limites remarquable. Les limites suivantes sont à connaître : lim. Preuve : Les démonstrations se font principalement en utilisant les propriétés de la fonction exponentielle. La fonction réciproque de logarithme népérien est la fonction exponentielle notée exp.
Les deux premiers résultats concernant les limites et la fonction logarithme sont donc : Remarque : on aurait également pu déduire ces résultats des limites de la. On peut noter exp x =ex pour tout x réel, avec e≃718. FONCTIONS LOGARITHMES. La touche finale de trois cours : exponentielle, logarithme et limites.
FICHE : LIMITES ET ÉQUIVALENTS USUELS. Pour vous aider avec les limites des fonctions ln (x) et exp (x). Cette fonction est appelée fonction exponentielle, on la note exp. Dérivée de la fonction . Si h désigne la composée de ln avec exp , le théorème des fonctions . Le tableau de variations de la fonction ln est : Propriétés.
Logarithmes et exponentielles. Exercice : Correction. Rappel : ln (2) ln (11). Etude de fonctions. Déterminer les asymptotes éventuelles de.