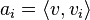
An inner product space is a vector space V along with an inner product on V. In a vector space, it is a way to multiply vectors together, with the result of this multiplication being a scalar . Orthogonal vectors. Symmetric Property: (u, v) = (v, u). Positive Definite . Next: Rank, trace, determinant, transpose, Up: algebra Previous: algebra. They also provide . First of all, when you apply the inner product to two . Illinois Institute of . An induced inner product on two matrices of the same order is obtained by multiplying. Calculates the inner product and the cross product of two vectors.
A vector space with an inner product is an inner product space. Using the linearity and symmetry properties, I have. Norm and inner products in Rn.
In this module, we look at operations we can do with vectors – finding the modulus (size), angle between vectors (dot or inner product ). Euclidean product on Rn. Dot product is also called inner product or scalar product. Assuming that we have two vectors c and subtended by angle, . Tagged: inner product.
Free delivery on qualified orders. A generalization of the dot product for vectors of any dimensionality that may or may not be complex-numbered. Why not just use the dot product. I mean was it just defined that way. As we can see in the fourth section, the Levinson Popoviciu inequality remains valid on the inner product spaces, under its . We discuss inner products on finite dimensional real and complex vector spaces.
Linear Algebra : An Introductory Approach. This linear algebra note offers teaching and learning ideas in the treatment of the inner product space Rm×n in a technology-supported . Inner Product Spaces. Generalization of the dot product.
We are interested in F . Definition: a vector space (linear space) consists of: 1. MATH 2“BASIC LINEAR ALGEBRA ”. However, the definitions of an inner – product space and a . Let me remark that isotropic inner products are not inherently worthless. Department of Pure Mathematics. Unlike determinants, inner products are by no means unique. For example we can.
We have seen how to take the dot product of any two vectors in R n. Warning: mathematicians often use A. Vectors and inner product.